Accueil › Cryptographie › D.E.S. – Data Encryption Standard en PowerShell

D.E.S. – Data Encryption Standard en PowerShell

Posté le de — Aucun commentaire ↓

Salut les gens !
Avant de commencer, j’espère que les TPs sur Enigma vous ont intéressés, et si vous les avez loupés : c’est par ici.

CrackingBoard
La machine à 250k$ de l’EFF pour péter Data Encryption Standard

Et pour ceux qui viennent d’arriver, je rappelle qu’on reprend ici les principaux algorithmes de cryptographie de l’histoire. Jusqu’ici on a vu, que des algorithmes de substitution (poly-)alphabétique avec César, Vigenère, et Enigma. On vous a aussi montré comment attaquer ces algorithmes à l’aide de propriétés statistiques : Fréquence des lettres ou indice de coïncidence ; le tout saupoudré d’un peu de brute-force.

Vous aviez aimé ? bien, parce que c’est fini, aujourd’hui on rentre (doucement) dans la cours des grands (avec des poils, et tout) et on commence avec un monument de Crypto Moderne : D.E.S. – Data Encryption Standard.

D.E.S., Data Encryption Quoi ?

Data Encryption Standard est le nom d’un algorithme datant de 1977 dans sa première version. Il fait suite à la demande du NBS (aujourd’hui appelé le NIST pour National Institute of Standards and Technology) d’un algorithme de chiffrement à destination des entreprises. C’est à peu de choses près la même histoire que pour AES (pour Advanced Encryption Standard) plus récemment, mais on y viendra.

Pour DES il s’est avéré qu’IBM avait déjà un algorithme qui répondait au besoin du NIST nommé « Lucifer« , et c’est presque lui qui fut rebaptiser en DES…. après un tout petit passage de rien du tout à la NSA (d’environ 3 ans).  Bon je vous passe déjà les doutes émis par la communauté à ce moment là sur les bonnes intentions de cette agence à but non lucratif vis à vis de l’algorithme. L’article Wikipédia explique d’ailleurs très bien  que rétrospectivement ce n’est pas aussi net qu’un affaiblissement volontaire, et que le passage à la NSA l’aurait plutôt durcit. Mon avis ? c’est qu’ils l’ont durci « juste ce qu’il » faut pour qu’eux puissent encore le casser simplement mais pas les autres.

Et à partir de là, est née Data Encryption Standard, dit « D.E.S. ». Pour quasiment trente ans de bons et loyaux services, quand on sait le temps qu’on mis en les entreprises à passer à AES à partir du 21ème siècle.

Data Encryption Standard, ou pas…

Petite digression pour ceux qui ne serait pas au courant : Il ne faut plus utiliser D.E.S. !!! C’est compris ? Rapidement, en fait à partir du début des années 90 on s’est rendu compte qu’il y avait plein de façons de trituré ce pauvre DES pour lui faire cracher tout ou une partie de ses clefs. Mais on y reviendra plus tard dans le TP sur comment casser Data Encryption Standard.

Complexité

Data Encryption Standard est un algorithme de chiffrement symétrique (je ne vous ai pas encore expliqué l’asymétrique je sais… mais ça viendra, ne soyez pas trop pressé non plus), ce qui veut dire qu’il prend en entrée:

  • une clé ; et
  • un bloc de donnée à chiffrer ou déchiffrer.

Et qu’on met ces deux entrées dans une fonction de chiffrement ou de déchiffrement selon ce qu’on veut faire, mais que dans les deux cas : la clé reste la même ! C’est un peu comme Enigma ou notre « clé » était la combinaison : tableau de connexion et choix plus ordre des rotors et positions initiales des rotors, et qui comme on l’a vu laisser tout de même : 2 .9x 10^22 clés à tester.

Ici la clé est un bloc de 64bits soit 8 octets (ou « bytes » en anglais), dont le dernier bit de chaque octets est utilisé pour le contrôle. Ce qui nous laisse un ensemble de 64 – 8 = 56 bits utilisables pour la clé. Et pour ceux qui ont eu 20/20 en théorie de l’information : ça fait très exactement 2^56 possibilités à tester pour la clés, soit en puissante de 10 : 7.2 x 10^16. Vous noterez que c’est moins que pour Enigma ! Sauf qu’on verra par la suite que ça reste beaucoup plus complexe à casser que la machine de la seconde guerre mondiale.

Implémentation (et permutations)

Alors comme on va le voir : dans Data Encryption Standard quand tu sais pas quoi faire : échanges des bits ! Plus sérieusement… l’algorithme D.E.S., se divise en 3 parties :

  1. Préparation de la clé
  2. Préparation des données
  3. « n » passages successif dans un chiffrement
  4. et « formatage » de la sortie.

Petite précision :

J’ai implémenté ici une version ECB – Electronic Code Book de D.E.S., ce qui signifie que si l’on chiffre 128bits de données, on va couper le message en 2 blocs de 64, qu’on chiffrera indépendamment, comme dans le schéma ci-dessous.

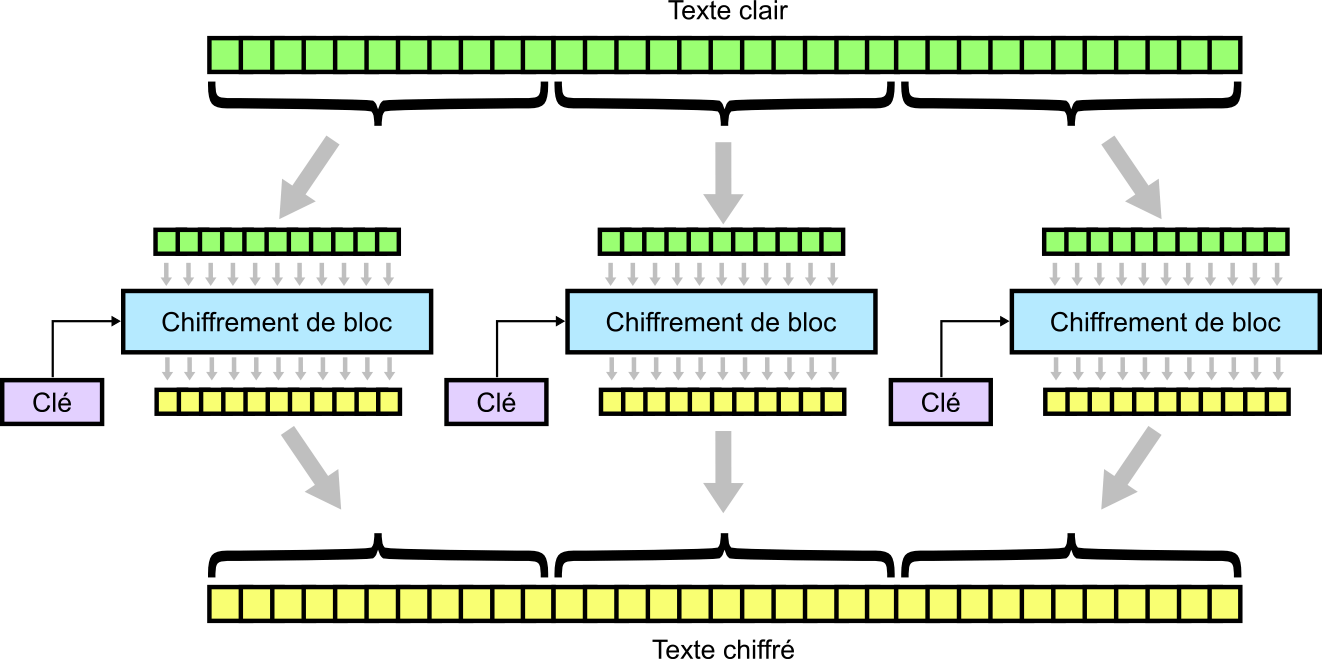
ECB - DES - Data Encryption Standard
Fonctionnement ECB

La grosse faiblesse du mode ECB est que deux blocs avec les mêmes données sont chiffrés à l’identique. Et ça c’est vraiment pas top en crypto… d’un autre côté, c’était un peu plus facile à implémenter ici (je suis faible je sais…)

Opérations de bases nécessaires à D.E.S.

Avant d’attaquer le vif du sujet, il a fallu définir tout un train de fonction de base nécessaire à la manipulation unitaire des bits dans les octets, qui n’était pas dispo nativement en PowerShell. Et sans transition donc :

# Converti un octet (Byte) en tableau de 8 bit (chacun de type octet car le "bit" n'existe pas en PowerShell).
Function ConvertFrom-ByteToBitArray{
    Param(
    $Byte = [Byte]::MinValue,
    [switch] $ParityBit = $false
    )
    $BitArray = [Byte[]] @(0,0,0,0,0,0,0,0)
    if($ParityBit){
        $p = [Byte] 0
        $bytesize = 7
    }else{
        $bytesize = 8
    }
    for($i=0;$i -lt $bytesize;$i++){
        $mask = [Byte][Math]::Pow(2,$i)
        $BitArray[$i]= [Byte]($Byte -bAnd $mask)/$mask
        if($ParityBit){
            $p = ($p + $BitArray[$i])%2
        }
    }
    if($ParityBit){
        $BitArray[$i] = $p
    }
    return $BitArray
}
# Inverse de ConvertFrom-ByteToBitArray, converti un tableau de bit en un octet (Byte).
Function ConvertFrom-BitArrayToByte{
 Param(
    [Byte[]] $BitArray = (new-object Byte[] 8),
    [switch] $ParityBit = $false
    )
    $Byte = 0
    $len = $BitArray.length
    if($ParityBit){
        $len -=1
    }# on ignore le dernier bi de parité si spécifié

    for($i=0;$i -lt $len;$i++){
        if($BitArray[$i] -eq 1){
            $Byte += [Byte][Math]::Pow(2,$i)
        }
    }
    return $Byte
}
# Fonction de niveau supérieur à ConvertFrom-ByteToBitArray; celle ci prend plusieurs octets en entrée et retourne le tableau de bits complet associé.
Function ConvertFrom-ByteArrayToBitArray{
    Param(
    [Byte[]] $Bytearray
    )
    $BitTab = $null
    for($i=0 ; $i -lt $Bytearray.length; $i++){
        $BitTab += (ConvertFrom-ByteToBitArray -Byte ([Byte] $Bytearray[$i])) #-ParityBit
    }
    return $BitTab
}
# Celle est une variante de l'opérateur PowerShell -shl qui fait un décale bit à bit vers la gauche (équivalent à un × 2), mais qui ne fait pas la version circulaire (où le bit en position 8 se retrouve en position 1).
Function Get-BitArrayCyclingLeftShift{
    Param(
    [Byte[]] $BitArray
    )
    $tmp = [Byte] $BitArray[0]
    for($i=0; $i -lt $BitArray.length - 1; $i++){
        $BitArray[$i] = [Byte] $BitArray[$i+1]
    }
    $BitArray[$i] = $tmp
    return $BitArray
}
# Idem, ré-implémentation de l'opérateur natif -bxor pour manipuler directement mes tableaux de bits. Et éviter ainsi un ballet incessant de conversion BitArrays <-> Bytes
Function Get-BitArrayXor{
    Param(
    [Byte[]] $BitArray1,
    [Byte[]] $BitArray2
    )
    $BitArrayRes = [Byte[]] @()
    if($BitArray1.length -eq $BitArray2.length){
        for($i=0; $i -lt $BitArray1.length; $i++){
            $BitArrayRes += [Byte] ($BitArray1[$i] -bxor $BitArray2[$i])
        }
    }
    return $BitArrayRes
}
# THE FONCTION dans Data Encryption Standard
DES-permutation
Les permutations, c’est la vie…
# implémente la permutation de bit dans un tableau de bits,
# par exemple si on entre :
#     0 0 0 1 0 0 0 1 avec la tableau de permutation 8 7 6 5 4 3 2 1; on obtiendra
#     1 0 0 0 1 0 0 0 
#(i.e b8 b7 b6 b5 b4 b3 b2 b1, par rapport à notre octet initial)
# pigé ?
Function Get-BitPermutation{
    Param(
    [Byte[]] $DataBitArray,
    [Byte[]] $PermutationTable

    )
    $PermutedData = [Byte[]] @()
    for($i=0;$i -lt $PermutationTable.count;$i++){
        $PermutedData += [Byte] $DataBitArray[($PermutationTable[$i])-1] # 1 pour index de départ à 1 dans les tableaux dans ce module DES
    }
    return $PermutedData
}

Et c’est tout ce dont on va avoir besoin pour l’instant…

Préparation des (sous) clés

Alors pour commencer, on doit préparer nos « sous-clés », c’est à dire passer de une unique clé de 56 bits (64 avec les bits de parités) à 16 clés de 48 bits.

Voici les opérations à réaliser :

  1. Permuter les bits de la clé K selon un tableau PC1 ;
  2. Séparer la clé en 2 morceaux de 32 bit : C0 et D0 tel que C = K0..27 et D = K28..55 ;
  3. Pour i de 1 à 16, faire :
    1. C1 = #Mi Décalages de bit circulaire à gauche (Ci-1)
    2. D1 = #Mi Décalages de bit circulaire à gauche (Ci-1)
      Ou M est un tableau indiquant le nombre de décalage pour chaque n°i
  4. Pour i de 1 à 16, faire :
    1. Kn = CnDn
    2. Permuter Kn selon un tableau PC2 (qui ne conserve que 48 bits sur les 56 en entrées)
  5. Retourner K1 à K16

Ce que je viens de décrire ici c’est un « key schedule » en Anglais. L’idée, c’est de mélanger et disperser suffisamment uniformément notre donnée initiale (la clé) de façon à ce qu’on ne puisse pas utiliser des propriétés statistiques pour la récupérer ensuite… tout en conservant un algorithme de préparation facile à inverser (c’est à dire récupérer la clé complète si on a toute les sous-clés). La bonne conception de cet algo est absolument critique pour garantir la résistance de l’algo à une cryptanalyse par la suite (mais on verra ça plus tard)…

Et donc le code associé :

Function Get-DESSubKeys{
    Param( 
    [Byte[]] $ByteKey
    )
    $BitTabKey = ConvertFrom-ByteArrayToBitArray $ByteKey
    #Permutation de la clé via PC-1
    #---------------------------------#
    $PermutationTablePC1 = [Byte[]] @(57,49,41,33,25,17,9,1,58,50,42,34,26,18,10,2,59,51,43,35,27,19,11,3,60,52,44,36,63,55,47,39,31,23,15,7,62,54,46,38,30,22,14,6,61,53,45,37,29,21,13,5,28,20,12,4)
    $PermutedKey = Get-BitPermutation -DataBitArray $BitTabKey -PermutationTable $PermutationTablePC1
    
    #Séparation en 2 moitié de la clé permutée
    #---------------------------------#
    $C = New-Object System.Collections.ArrayList
    $D = New-Object System.Collections.ArrayList
    $C.Add([Byte[]]$PermutedKey[0..27]) | out-null
    $D.Add([Byte[]]$PermutedKey[28..55]) | out-null

    #Et création des 16 sous binone de "pré-sous-clés" associées
    #---------------------------------#
    $ShiftCountTable = @(1,1,2,2,2,2,2,2,1,2,2,2,2,2,2,1)
    for($i=1;$i -le 16;$i++){
        $tmpC = ($C[$i-1]).Clone()
        $tmpD = ($D[$i-1]).Clone()
        for($j=0;$j -lt $ShiftCountTable[$i-1];$j++){
            $tmpC = Get-BitArrayCyclingLeftShift -BitArray $tmpC
            $tmpD = Get-BitArrayCyclingLeftShift -BitArray $tmpD
        }
        $C.Add($tmpC) | out-null
        $D.Add($tmpD) | out-null
    }

    # et on forme enfin les sous-clés K en re-concaténant CnDn suivi avec d'une dernière permutation
    #---------------------------------#
    $K = New-Object System.Collections.ArrayList
    $Ktmp = New-Object System.Collections.ArrayList
    # Tableau de permutation n°2 de la clé : PC-2
    $PermutationTablePC2 = [Byte[]] @(14,17,11,24,1,5,3,28,15,6,21,10,23,19,12,4,26,8,16,7,27,20,13,2,41,52,31,37,47,55,30,40,51,45,33,48,44,49,39,56,34,53,46,42,50,36,29,32)
    for($i=0;$i -le 16;$i++){
        $Ktmp.Add(($C[$i]+$D[$i]).Clone()) | out-null
        $PermutedK = Get-BitPermutation -DataBitArray $Ktmp[$i] -PermutationTable $PermutationTablePC2
        $K.Add($PermutedK) | out-null
    }
    #---------------------------------#
    #Et c'est bon pour la sous clé !!! mais easy quoi...
    Write-Verbose 'Sous-clés préparé'
    Return $K
}

Et donc à ce moment j’ai 16 sous clés de 48bits prête à l’usage, en faisant un simple appel à :

$K = Get-DESSubKeys $ByteKey

Chiffrement des données

Préparation des données

D.E.S. chiffre des blocs de données de 64bits, sauf que notre utilisateur qui a écrit le texte à chiffrer ne s’est pas embêter à écrire un texte dont la longueur en octets est un multiple de 64 bits. Donc on va « bourrer » nos données avec des zéros à la fin pour arriver jusqu’à une longueur  multiple de 64bits. Comme ça:

While((($Msg.length)*8)%64 -ne 0){
    $Msg += [Byte] 0
}
$ByteMsg = $Msg

Vous suivez jusqu’ici ?

Traitement des blocs de données

Alors comme pour le traitement de la clé, avant de commencer je vous donne l’algorithme avant l’implémentation :

Pour chaque bloc B (de 64 bits) du message :

  1. Permuter les bits du bloc selon un tableau IP ;
  2. Séparer le message en deux morceaux L0 et R0 (pour Left/gauche et Right/droite) tel que L0 = B1..32 et R0 = B33..64 ;
  3. Pour i de 1 à 16, faire :
    1. Li = Ri-1 ;
    2. Ri = Li-1 « xor » F(Ri-1, Ki) ; ou F est détaillée plus bas ;
  4. Concaténer R16 et L16 dans un bloc chiffré C ;
  5. Permuter les bits de C selon le tableau inverse de IP : IP-1 ;
  6. Ajouter C au message chiffré et passer au bloc suivant ;

Retourner l’ensemble des blocs chiffré mis bout à bout.

Au final en Powershell ça donne ça :

Function Get-DESCypher{
    [CmdletBinding()]
    Param(
        [Byte[]] $Key = (19,52,87,121,155,188,223,241), # note : des octets de "7 bits", car le dernier bit est remplacé par la parité des 7 premiers (et devrait l'être dès le départ en fait).
        [Byte[]] $Msg = @(1,35,69,103,137,171,205,239)
    )
    #Mode ECB : Electronic Code Book
    #2 autres modes : Chain Block Coding (CBC) and Cipher Feedback (CFB), which make each cipher block dependent on all the previous messages blocks through an initial XOR operation.

    #Préparation de la Clé en "SubKeys"
    #---------------------------------#
    #La clé en tableau de bit
    $K = Get-DESSubKeys $Key #$K est Tableau de 17 élément de K1 à K16 (+ n°0 inutile mais renvoyé)

    #Traitement du message par bloc de 64 bits
    #-----------------------------------------#
    #déjà on 'pad' le message avec des '0' pour obtenir un multiple de 64bits.
    While((($Msg.length)*8)%64 -ne 0){
        $Msg += [Byte] 0
    }
    $ByteMsg = $Msg
    $CypheredBitArray = $null
    for($i=0;$i -lt $ByteMsg.Length; $i+=8){

        # Pour chaque bloc de 64bit du message - ECB
        $MBloc = $ByteMsg[$i..($i+7)]
        Write-Verbose "Traitement du bloc de message : $i à $($i+7)"
        #Conversion en bit
        $BitTabMsgBloc = ConvertFrom-ByteArrayToBitArray $MBloc
        
        # On permute selon la table IP
        $PermutationTableIP = @(58,50,42,34,26,18,10,2,60,52,44,36,28,20,12,4,62,54,46,38,30,22,14,6,64,56,48,40,32,24,16,8,57,49,41,33,25,17,9,1,59,51,43,35,27,19,11,3,61,53,45,37,29,21,13,5,63,55,47,39,31,23,15,7)
        $PermutedMsgBloc = Get-BitPermutation -DataBitArray $BitTabMsgBloc -PermutationTable $PermutationTableIP

        #Préparation de l'application des clés sur les blocs de données
        $L = New-Object System.Collections.ArrayList
        $R = New-Object System.Collections.ArrayList
        $L.Add([Byte[]]$PermutedMsgBloc[0..31]) | out-null
        $R.Add([Byte[]]$PermutedMsgBloc[32..63]) | out-null

        #Application des 16 sous-clés au bloc de données
        for($j=1;$j -le 16;$j++){
            $L.Add($R[$j-1].clone()) | out-null
            $R.Add((Get-BitArrayXor -BitArray1 ($L[$j-1]) -BitArray2 (Get-FuncDES -R $R[$j-1] -K $K[$j]))) | out-null
        }
        #Bloc presque chiffré avec les 2 dernier demi-blocs de 32bits
        $tmp = @($R[16]+$L[16])

        #Dernière permutation de bits
        $PermutationTableIP_1 = @(40,8,48,16,56,24,64,32,39,7,47,15,55,23,63,31,38,6,46,14,54,22,62,30,37,5,45,13,53,21,61,29,36,4,44,12,52,20,60,28,35,3,43,11,51,19,59,27,34,2,42,10,50,18,58,26,33,1,41,9,49,17,57,25)
        $CypheredBloc = Get-BitPermutation -DataBitArray $tmp -PermutationTable $PermutationTableIP_1

        #Et on construit le résultat
        $CypheredBitArray += $CypheredBloc
        Write-Verbose "Chiffré en $($CypheredBitArray.count) bits : $CypheredBitArray"

    }

    #Que l'on converti à nouveau en Byte[]
    $Cypher = [Byte[]] @()
    for($k=0;$k -lt $CypheredBitArray.length;$k+=8){
        $Cypher += (ConvertFrom-BitArrayToByte $CypheredBitArray[$k..($k+7)])
    }
    Return [Byte[]] $Cypher
}

Facile, non ? ça tient en moins de 100 ligne…

Mais je vais pas m’en tirer comme ça, il me reste quand même à détailler cette fonction F que j’ai appelé Get-FuncDES dans le code.

La fonction F (pour Feistel) de D.E.S.

Expansion

Les quelques uns d’entre-vous qui suivent encore jusqu’ici auront notés que dans F on entre la clé Ki et  le bloc Ri-1…On se doute que dans F, on va mélanger ces deux  ensembles de bits via une opération réversible si on a les 2 éléments (mais pas si on en a qu’un) pour  faire le chiffrement. Sauf que ces 2 éléments n’ont pas la même taille : Ki fait 48 bits alors que les Ri n’en font que 32. La première étape va donc être donc d’étendre Ri sur 48 bits, ce qui correspond en fait à une permutation de bits particulière ou l’on a plus de bit à permuter que dans l’entrée. D’où la définition de cette fonction :

Function Get-DESExpand{
    Param( 
    [Byte[]] $R
    )
    #Etendre 32bit sur 48 à l'aide d'un table d'expansion fixe
    $EBitSelectionTable = @(32,1,2,3,4,5,4,5,6,7,8,9,8,9,10,11,12,13,12,13,14,15,16,17,16,17,18,19,20,21,20,21,22,23,24,25,24,25,26,27,28,29,28,29,30,31,32,1)
    #en fait c'est une permutation particulière ou on ajoute de la donnée 
    $ExpandedR = Get-BitPermutation -DataBitArray $R -PermutationTable $EBitSelectionTable
    return $ExpandedR
}

Ensuite on va tout simplement faire un Ou-Exclusif entre K et R; pour avoir de la donnée chiffrée via notre clé Ki.

S-Box ou Boites-S

Ensuite et c’est là ou ça devient nouveau et un peu perturbant, Data Encryption Standard utilise un mécanisme de Boites-S pour « brouiller » le résultat du Xor ci-dessus. Une boite-S est simplement une boite noire qui mélange encore un peu plus nos données. Ça ressemble un peu à une permutation mais en deux dimensions. Pour Data Encryption Standard elles ont étés conçus de la manière suivante :

Pour un bloc de 6 bits, le premier et le dernier bit du bloc correspondent à l’indice des lignes dans un tableau S alors que les 4 bits du milieu donne l’indice des colonnes.

Par exemple si on a le bloc suivant : « 011011 »; le premier et le dernier bit font « 01 »=1 et les quatre bits du milieu « 1101 » font 13 (A noter que ça diffère si vous comptez en Big-Endian ou Little-Endian); dont pour ce qui ce substitura à nos six bit sera l’élément S[1][13] dans la S-Box.

Dans DES on a une S-Box par bloc de six bits issue de l’expansion et chiffrement de l’étape d’avant qui nous retourne une valeur sur 4 bits; ce qui fait qu’en sortie on retrouve bien 32 bits. Voici la n°1 utilisée pour les 6 premiers bits donc :

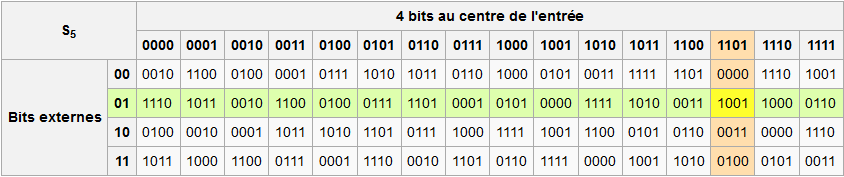
S-Box1DES
S-Box n°1 sur 8 dans DES

Ce qui est assez surprenant : c’est que si je vous donne 4 bits en entrée de la S-box vous ne pouvez pas retrouvez la ligne et la colonne associé. Mais que pourtant DES arrive à retrouver ses petits au déchiffrement, ce qui implique qu’elles soient bien conçus pour votre algorithme et pas simplement tirées au hasard pour ne pas perdre de données.

Du coup ça nous donne la fonction suivante pour gérer les huit S-Box de Data Encryption Standard

Function Get-SBoxes{
    Param( 
    [Byte[]] $SixBitArray,
    [Byte] $BoxNum #0 - 7
    )
    $S1 = @((14,4,13,1,2,15,11,8,3,10,6,12,5,9,0,7),(0,15,7,4,14,2,13,1,10,6,12,11,9,5,3,8),(4,1,14,8,13,6,2,11,15,12,9,7,3,10,5,0),(15,12,8,2,4,9,1,7,5,11,3,14,10,0,6,13))
    $S2 = @((15,1,8,14,6,11,3,4,9,7,2,13,12,0,5,10),(3,13,4,7,15,2,8,14,12,0,1,10,6,9,11,5),(0,14,7,11,10,4,13,1,5,8,12,6,9,3,2,15),(13,8,10,1,3,15,4,2,11,6,7,12,0,5,14,9))
    $S3 = @((10,0,9,14,6,3,15,5,1,13,12,7,11,4,2,8),(13,7,0,9,3,4,6,10,2,8,5,14,12,11,15,1),(13,6,4,9,8,15,3,0,11,1,2,12,5,10,14,7),(1,10,13,0,6,9,8,7,4,15,14,3,11,5,2,12))
    $S4 = @((7,13,14,3,0,6,9,10,1,2,8,5,11,12,4,15),(13,8,11,5,6,15,0,3,4,7,2,12,1,10,14,9),(10,6,9,0,12,11,7,13,15,1,3,14,5,2,8,4),(3,15,0,6,10,1,13,8,9,4,5,11,12,7,2,14))
    $S5 = @((2,12,4,1,7,10,11,6,8,5,3,15,13,0,14,9),(14,11,2,12,4,7,13,1,5,0,15,10,3,9,8,6),(4,2,1,11,10,13,7,8,15,9,12,5,6,3,0,14),(11,8,12,7,1,14,2,13,6,15,0,9,10,4,5,3))
    $S6 = @((12,1,10,15,9,2,6,8,0,13,3,4,14,7,5,11),(10,15,4,2,7,12,9,5,6,1,13,14,0,11,3,8),(9,14,15,5,2,8,12,3,7,0,4,10,1,13,11,6),(4,3,2,12,9,5,15,10,11,14,1,7,6,0,8,13))
    $S7 = @((4,11,2,14,15,0,8,13,3,12,9,7,5,10,6,1),(13,0,11,7,4,9,1,10,14,3,5,12,2,15,8,6),(1,4,11,13,12,3,7,14,10,15,6,8,0,5,9,2),(6,11,13,8,1,4,10,7,9,5,0,15,14,2,3,12))
    $S8 = @((13,2,8,4,6,15,11,1,10,9,3,14,5,0,12,7),(1,15,13,8,10,3,7,4,12,5,6,11,0,14,9,2),(7,11,4,1,9,12,14,2,0,6,10,13,15,3,5,8),(2,1,14,7,4,10,8,13,15,12,9,0,3,5,6,11))

    $Sboxes = New-Object System.Collections.ArrayList
    $Sboxes.Add($S1) | out-null
    $Sboxes.Add($S2) | out-null
    $Sboxes.Add($S3) | out-null
    $Sboxes.Add($S4) | out-null
    $Sboxes.Add($S5) | out-null
    $Sboxes.Add($S6) | out-null
    $Sboxes.Add($S7) | out-null
    $Sboxes.Add($S8) | out-null

    $ligIndex = ConvertFrom-BitArrayToByte @($SixBitArray[0],$SixBitArray[5])
    $colIndex = ConvertFrom-BitArrayToByte @($SixBitArray[1..4])

    $tmp = $Sboxes[($BoxNum)][$ligIndex][$colIndex]
    $Res = (ConvertFrom-ByteToBitArray ([Byte] $tmp))[0..3]
    return $Res
}

Note pour la suite : Dans la Cryptanalyse différentielle, c’est la probabilité d’occurrence(s) de sorties de ces S-Box qui est attaquée pour retrouver la clé à partir d’entrée choisit intelligemment. Enfin on verra ça plus tard.

Dans le doute… permute

Et comme ça faisait longtemps avant de retourner nos 32 bits on va les mélanger encore un peu plus via une n-ième table de permutation.

Implémentation de F

A la fin la fonction est dont la suivante :

Function Get-FuncDES{
    Param( 
        [Byte[]] $R,
        [Byte[]] $K
    )
    $ExpandedR = Get-DESExpand -R $R
    $Xored = Get-BitArrayXor -BitArray1 $ExpandedR -BitArray2 $K

    # Sboxes :
    $SBitResult = [Byte[]] @()
    for($i=0; $i -lt $Xored.length; $i+=6){
        $SixBits = $Xored[$i..($i+5)]
        $SBitResult += (Get-SBoxes -SixBitArray $SixBits -BoxNum ($i/6))
    }

    #Permutation... pour changer
    $PermutationTableP = @(16,7,20,21,29,12,28,17,1,15,23,26,5,18,31,10,2,8,24,14,32,27,3,9,19,13,30,6,22,11,4,25)
    $Final = Get-BitPermutation -DataBitArray $SBitResult -PermutationTable $PermutationTableP
    
    return $Final
}

Test de fonctionnement

Bon, et ça marche ?

#Le message et la clé (si y'a rien qui vous choque dans mon choix là, réfléchissez bien)
$Message = [Byte[]] ('Les sanglots longs des violons de l''automne, blessent mon coeur d''une langueur monotone.'.ToCharArray())
$Key = [Byte[]] ('DDAY6644'.ToCharArray())

#Chiffrement
$chiffre = Get-DESCypher -Key $Key -Msg $Message

#Affichage en chiffré
[System.Text.Encoding]::ASCII.GetString($chiffre)
"?;?'??Sl~?♣K#?.rn?????oZ\⌂f∟??R??~???IS????~M?g?↑'?↕J???♥?3O=?NV??WVZP??'?????◄?@??J?HW"
#Affichage b64 : [System.Convert]::ToBase64String($chiffre)

#Chiffrement
$dechiffre = Get-DESDecypher -Key $Key -CypherMsg $chiffre
#Affichage déchiffré
[System.Text.Encoding]::ASCII.GetString($dechiffre)
"Les sanglots longs des violons de l'automne, blessent mon coeur d'une langueur monotone."

Et ça marche !

Déchiffrement de D.E.S.

Alors je vais pas vous refaire l’article pour le déchiffrement, là. An fait l’algo est strictement le même, à quelques nuances près. On va toujours faire 16 tours avec les mêmes clé et le message chiffré (à la place du message clair). mais dans l’autre sens, c’est à dire de la clé 16 à 1 et en inversant au départ L et R, soit l’algorithme suivant (j’ai mis en bleu les différence avec le chiffrement) :

Pour chaque bloc B (de 64 bits) du chiffré:

  1. Permuter les bits du bloc selon un tableau IP ;
  2. Séparer le message en deux morceaux L16 et R16 tel que L16 = B33..64 et R16 = B1..32 ;
  3. Pour i de 16 à 1, faire :
    1. Ri-1 = Li ;
    2. Li-1 = Ri « xor » F(Li, Ki) ; ou F est détaillée plus bas ;
  4. Concaténer L0 et R0 dans un bloc déchiffré C ;
  5. Permuter les bits de C selon le tableau inverse de IP : IP-1 ;
  6. Ajouter C au message déchiffré et passer au bloc suivant ;

Retourner l’ensemble des blocs déchiffré mis bout à bout.

Et comme je suis un salaud, je vais vous le laisser en exercice pour voir si vous avez tout bien compris :

Déchiffrez-moi donc ça (la clé est la même que tout à l’heure, et c’est encodé en base 64) :

xxU13tNZKn1IlMJxhSCmaQ0p+iun9HW39m90eSeBgXOk3lOiqFXAsb5WdkNX3d1SkFgvX669ebSXXcec1xD+1vKQ+8bjS6Kgtefqa4jAalWq/eYH2e
5z4OIBqoGvN0PX+U1UziZ1pmPn/k+XNjQR6/73STFIKuf4DKdn29CXZDHU7vUxiZwUxXLhmbjWZphVOtFPv1nuMXWudZxS1WUiUIVpwCtdCHOpvHWA
wiCkK1c=

Conclusion

Bon je vais dépasser les 3000 mots avec la conclusion, là. S’il fallait conclure sur Data Encryption Standard lui même, je vous rappellerai de ne pas l’utiliser et de privilégier AES. En terme de fonctionnement il faut avoir compris :

  • le système de sous-clé ;
  • Les permutations bit à bit ;
  • Le Xor ;
  • Comment marche une S-Box ; et
  • Le système de 16 itérations à partir de tout ça.

J’espère comme d’habitude vous avoir appris des trucs. Je vous avez prévenu au départ, la on attaque la crypto « moderne » (pour ce que ça veut dire), donc ça commence à s’adresser plus aux informaticiens qu’à M. Tout-Le-Monde. En tout cas je me suis régalé à vous sortir ça moi, même si j’y ai passé un bon bout de temps pour tout bien comprendre.

Pour la suite j’ai commencé à regarder la cryptanalyse différentielle sur D.E.S., mais alors là : ça pique beaucoup. Donc attendez pas l’article sur l’attaque avant petit moment.

Merci à ceux qui ont pris le temps de lire jusqu’au bout (et aux autres aussi, même si vous êtes faibles),

et @++

Laisser un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *

Ce site utilise Akismet pour réduire les indésirables. En savoir plus sur comment les données de vos commentaires sont utilisées.