Enigma, Quèsaco ?

Comment la machine est-elle apparue ?

Un peu d’histoire…

Durant la première guerre mondiale, les allemands utilisaient le code ADFGVX pour chiffrer leurs messages. Il faut savoir que ce chiffrement était fait à la main par un soldat, il n’était donc pas possible de l’utiliser à grande échelle. Durant cette guerre, les anglais avaient réussi à décrypter ce code, et connaissaient alors les prochains mouvements de l’ennemi. Ils en ont donc tiré parti pour vaincre l’Allemagne.

Lors de la Seconde Guerre Mondiale, les Allemands ont voulu à tout prix éviter la guerre de position, très meurtrière et peu efficace. Ils ont décidé d’adopter la « guerre de mouvement » ou les avions attaquent l’arrière des lignes, pendant que l’infanterie et les chars attaquent le front sur une vaste étendue. Mais pour pouvoir coordonner cela, il leur a fallu trouver un moyen de communication, rapide et chiffré afin de pouvoir déployer leur force rapidement, sans que leurs ennemis en aient connaissance.

L’homme à l’origine de la machine allemande est Arthur Scherbius, qui déposa le brevet en 1918. Elle ne fut pas utilisée par les militaires tout de suite à cause de l’armistice. Elle fut donc d’abord commercialisée publiquement. Cette machine présentait l’avantage de posséder un réflecteur qui permettait le déchiffrement du message rapidement et facilement.

La marine Allemande, après avoir compris que leur code ADFGVX était d’une piètre sécurité, décida de s’équiper d’Enigma à partir de 1926. En 1945, l’armée Allemande comptait près de 200 000 machines.

Il faut savoir qu’il existe plusieurs versions d’Enigma, à usage public ou militaire, plus ou moins complexe. La première fut la machine standard Enigma (militaire) et la machine Enigma D (public) qui est composé de trois rotors dans le brouilleur. Ensuite, à partir de 1933, nous avons la version militaire Enigma M3 qui est composé de trois rotors à choisir parmi cinq dans le brouilleur. Puis en 1942 est apparu l’Enigma M4, composé de trois rotors à choisir parmi huit et d’un rotor supplémentaire fixe à choisir parmi deux autres. Enfin, nous avons la machine Enigma G, qui fut utilisé par les services secrets allemands. Elle est composée de quatre rotors mais ne possède pas de tableau de fiche.

Dans un premier temps, nous allons donc chercher à comprendre comment fonctionne cette machine, et qu’est ce qui en a fait une force pour l’armée allemande pendant plusieurs années. Puis nous chercherons à décrypter un message codé par Enigma.

Comment que ça marche ce machin ?

Nous nous intéresserons au fonctionnement de la machine M3. Celle-ci est constituée historiquement de cinq parties :

1. Un réflecteur fixe ;
2. Trois rotors mobiles à choisir parmi cinq ;
3. Un affichage lumineux pour afficher la lettre chiffrée ;
4. Un clavier à touches pour taper la lettre à chiffrer ; et
5. Des fiches qui relient deux lettres entre eux, ce qui permet de les intervertir. Historiquement il y avait six fiches.

Lorsqu’on appuie sur une touche, un circuit électrique se ferme et le courant peu passer. Celui-ci va passer dans la succession de rotor puis va passer dans le réflecteur, avant de passer dans les rotors dans le sens inverse pour ensuite allumer une diode sur le tableau lumineux affichant la lettre chiffrée. Exemple ici.

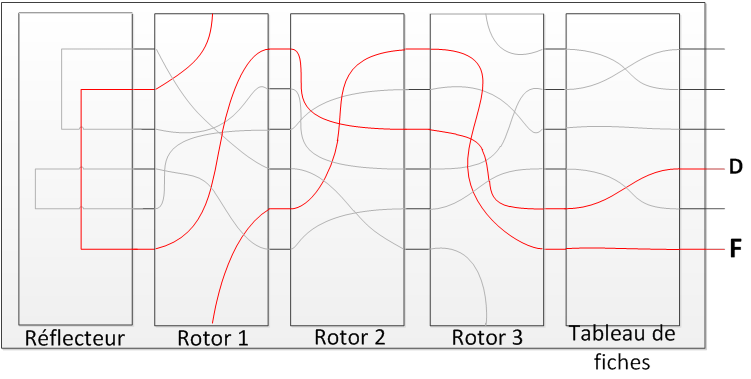
Les rotors servent à substituer mono alphabétiquement chaque lettre. La rotation du rotor permet de faire tourner la correspondance entre le circuit d’entré et le circuit de sortie. Par exemple, ici le A est chiffré en C, mais après une rotation le A deviendra un F. Un rotor permet donc de faire 26 alphabets chiffrés différents (substitution poly-alphabétique).

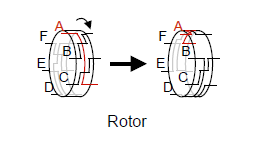
Mais pour éviter une attaque par statistique,  les rotors tournent. C’est-à-dire qu’avec un seul rotor il faudrait attendre 26 lettres avant d’avoir une seconde lettre chiffré avec le même alphabet chiffré. 26 lettres étant peu par rapport à un message, les allemands ont mis deux autres rotors, ce qui fait 26×26×26 avant la répétition d’un lettre chiffrée avec le même alphabet, soit 17576 lettres, ce qui est énorme pour un message. De plus, les allemands avaient la consigne de diviser les long messages en plusieurs petits pour éviter ce problème.

À l’entrée et à la sortie du brouilleur se trouve un tableau de fiche, permettant de permuter deux lettres entre elle.

Enigma : La complexité de la bestiole

Rotors :

26 positions de départ possible pour chaque rotors : car l’on a 26 positions de départ différentes pour chacun des trois rotors.

3 rotos à choisir parmi 5 :

Puis, la position des rotors entre eux = 3×2×1=6

Nombre de possibilités = 17576×60×6 = 6 327 360

Les fiches :

Nous avons donc six fiches pour vingt-six lettres :

Pour la première fiche : Le premier bout peut être relié à une des 26 lettres de l’alphabet, et le deuxième à une des 25 restantes. On a donc 26×25 possibilités pour la première fiche. Si on fait de même pour toutes les fiches on a alors

Complexité

La complexité finale est donc de

(possibilités de clés différentes).

On comprend bien qu’à la main cela peut être long. Par exemple, en raison d’un essai par seconde, il faudrait :

ans pour tous tester !

Heureusement pour nous, il y a des astuces pour ne pas avoir à tout tester. On verra cela par la suite.

Le programme de chiffrement

Comment chiffre-t-on ?

Tout d’abord il faut choisir la configuration de la machine. Celle-ci est composée de 4 parties :

• Les fiches ; ex (‘AV’,’DE’,’HO’,’JK’,’LS’,’XQ’)
• Les rotors utilisés et leur ordre ; ex (‘I’,’VI’,’II’)
• Les positions initiales des rotors ; ex (25, 6, 4)
• Le réflecteur utilisé. Ex ‘RefB’

Durant la seconde guerre mondiale, cette configuration d’Enigma était écrite dans un cahier, qui était dupliqué et transmis à toute l’armée allemande. Ainsi tout le monde avait la même clé. Celle-ci était valable pour une durée de 8h à 2 jours selon les armées.

Historiquement, le chiffreur choisissais ensuite trois lettres (ex : COU) et tapait cette clé deux fois sur la machine afin d’éviter les erreurs de frappe. Il obtenait ainsi une clé chiffrée (ex : COUCOU -> DEROMK). Ensuite, il changeait les positions initiales des rotors par la clé choisie : ex C -> 3, O -> 15, U ->21, il mettait donc les rotors sur 3, 15, 21. Puis il tapait le message à chiffrer.

Le message transmis était sous la forme :

- 25 6 4 - DEROMK

MESSA GECOD EEPAR ENIGM AETTR ANSMX ISAUX ALLEM ANDSX MESSA GECOD EEPAR ENIGM AETTR ANSMX ISAUX ALLEM ANDSX MESSA GECOD EEPAR ENIGM AETTR ANSMX ISAUX ALLEM ANDSX MESSA GECOD EEPAR ENIGM AETTR ANSMX ISAUX ALLEM ANDSX MESSA GECOD EEPAR ENIGM AETTR ANSMX ISAUX ALLEM ANDSX MESSA GECOD EEPAR ENIGM AETTR ANSMX ISAUX ALLEM ANDSX MESSA GECOD EEPAR ENIGM AETTR ANSMX ISAUX ALLEM ANDSX MESSA GECOD EEPAR ENIGM AETTR ANSMX ISAUX ALLEM ANDSX MESSA GECOD EEPAR ENIGM AETTR ANSMX ISAUX ALLEM ANDSX MESSA GECOD EEPAR ENIGM AETTR ANSMX ISAUX ALLEM ANDSX

Mais la première ligne fut rapidement supprimée car cela formait une faille, que les polonais ont exploitée pour la cryptanalyse de la machine.

Le code en PowerShell :

Voici une proposition d’implémentation de la machine Enigma en Powershell.

Constantes :

# On ne génère par les rotors aléatoirement, car nous voulons nous rapprocher de la version historique, nous utilisons donc les rotors historiques de la version M3
# De plus, si on les générait aléatoirement il faudrait envoyer ces dispositions à notre correspondant.
$Rotors = @{
    'alphabet'  = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ';
    'I'         = 'EKMFLGDQVZNTOWYHXUSPAIBRCJ';
    'II'        = 'AJDKSIRUXBLHWTMCQGZNPYFVOE';
    'III'       = 'BDFHJLCPRTXVZNYEIWGAKMUSQO';
    'IV'        = 'ESOVPZJAYQUIRHXLNFTGKDCMWB';
    'V'         = 'VZBRGITYUPSDNHLXAWMJQOFECK';
    'RefB'      = 'YRUHQSLDPXNGOKMIEBFZCWVJAT';
    'RefC'      = 'RDOBJNTKVEHMLFCWZAXGYIPSUQ'
}

$R = [int][char]'R'- [int][char]'A'
$F = [int][char]'F'- [int][char]'A'
$W = [int][char]'W'- [int][char]'A'
$K = [int][char]'K'- [int][char]'A'
$A = [int][char]'A'- [int][char]'A'

# Ceci est le tableau des rotations de rotors. Par exemple, pour le rotor I, il va faire tourner le rotor à sa gauche de 1 quand il passera de de Q à R
$changementsRotors = @{
    'I'    = @($R);
    'II'   = @($F);
    'III'  = @($W);
    'IV'   = @($K);
    'V'    = @($A);
}

Variables :

# Représente les fiches. Une lettre ne peut apparaitre qu’une seule fois.
# Historiquement il y avait 6 ou 10 fils.
$tabconnexion    = @('AW','HX','CO','JP','EK','FR') 

# Un tableau représentant les rotors utilisés et leur ordre.
# rotor 1 : IV ; rotor 2 : I ; rotor 3 : III
$RotorSetup      = @('IV','I', 'III')        

# Les positions initiales des rotors.
$RotorInitPos    = @(7, 25, 17)

# Le réflecteur utilisée 
$Reflector       = 'RefB'
$MessageAChiffre = “ Bonjour je m’appelle Uni Kitty ”

Pour toutes les lettres du texte à chiffrer, il faut faire le parcours suivant :

Passage par la table de connexion (aller) :

Avec la table de connexion que l’on a mis en paramètre au-dessus, si l’on tape A, on aura W.

Foreach($connexion in $tabconnexion){
    if($letter -eq $connexion[1]){
       $letter = $connexion[0]
       break;
    } elseif ($letter -eq $connexion[0]) {
       $letter = $connexion[1]
       break;
    }
}

Passage dans les rotors (aller) :

On parcourt les rotors comme cela : Rotor 3 -> Rotor 2 -> Rotor 1 (de droite à gauche).

Exemple : On a la lettre W en entrée. Les rotors sont de haut en bas : Alphabet, rotor (Attention, petite erreur : il y a eu une inversion entre le rotor IV et III dans le tableau, la logique reste la même, c’est un exemple.)

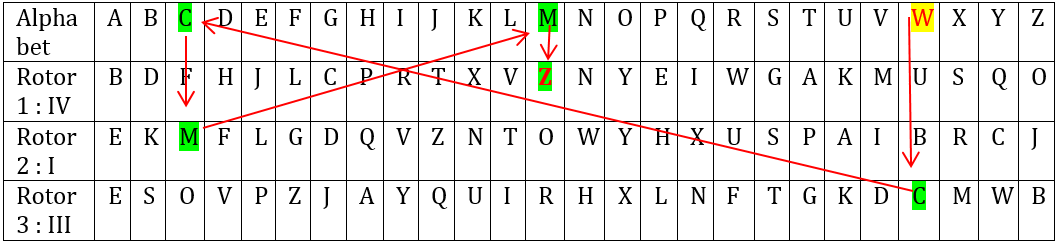
On obtient un Z.

# Note : au départ RotorPos[$i] = RotorInitPos[$i]
for($i = $RotorSetup.count-1; $i -ge 0;$i--){
   $Rotor = $RotorSetup[$i]
   $pos = $Rotors.'alphabet'.IndexOf($letter)
   $letter = $Rotors."$Rotor"[($pos + $RotorPos[$i])%($Rotors.'alphabet'.length)]
}

Passage dans le réflecteur :

Exemple si on a la lettre Z (2 méthodes de recherche) :

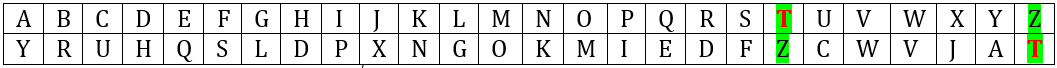
Cela nous donne donc la lettre T.

$letter = $Rotors.'alphabet'[$Rotors.$Reflector.IndexOf($letter)]

Passage dans les rotors (retour) :

On parcourt les rotors selon cet ordre : Rotor 1 -> Rotor 2 -> Rotor 3 (de gauche à droite). Attention ici on passe dans le sens inverse !

Exemple, avec un T en entrée :

On obtient un F.

for($i = 0; $i -lt $RotorSetup.count;$i++){
    $Rotor = $RotorSetup[$i]
    $pos = (($Rotors.'alphabet'.length) 
          + ($Rotors.$Rotor.IndexOf($letter) 
          - $RotorPos[$i]))%($Rotors.'alphabet'.length)
    $letter = $Rotors.'alphabet'[$pos]
}

Passage dans la table de connexion (Retour) : Voir aller

Avec la table de connexion que l’on a, notre F sera transformé en R. Voici comment notre A a été transformé en R par la machine.

Il suffit maintenant de faire cela avec toutes les lettres de notre message.

Le déchiffrement

Enigma a la propriété d’être très facilement déchiffrable grâce à son réflecteur. Lorsqu’on a le texte chiffré et la configuration de la machine, il suffit de taper le texte chiffré pour l’avoir en clair. On a donc :

Pourquoi ?

Le réflecteur sert à rendre le circuit symétrique. C’est-à-dire que pour une même position, si l’on tape A et que l’on obtient D alors en tapant D on obtiendra A.

Le réflecteur d’Enigma a grandement simplifié le déchiffrement mais a aussi inclus une faiblesse : Une lettre ne peut jamais être codée par elle-même.

Donc le programme de déchiffrement est le même que celui de chiffrement, sauf qu’on met en entrée le texte chiffré.

Conclusion

Nous avons appris comment chiffrer un texte grâce à Enigma. Nous nous attaquerons dans le prochain TP à la cryptanalyse d’Enigma.